NOTA
SUMBER:http://addmathnhhs.blogspot.com/p/nota-nota.html
Bab 1 : Fungsi
1. Fungsi ialah sejenis hubungan khas yang mana setiap objek dalam domain mempunyai hanya satu imej dalam kodomain.
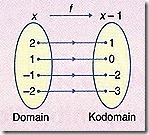

Hubungan satu dengan satu Hubungan satu dengan satu
ialah fungsi ialah fungsi
2. Fungsi nilai mutlak ditakrifkan oleh
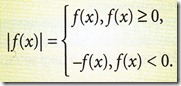

Graf fungsi nilai mutlak
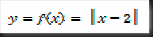
3. Jika f ialah suatu fungsi yang memetakan set A kepada set B dan g ialah suatu fungsi yang memetakan set B kepada set C, maka gf ialah fungsi gubahan f diikuti dengan g yang memetakan set A terus kepada set C.

4. Jika ialah suatu fungsi yang memetakan x kepada y, maka songsangannya ditandakan sebagai f-1. Fungsi songsang ialah suatu fungsi yag memetakan y kembali kepada x.
ialah suatu fungsi yang memetakan x kepada y, maka songsangannya ditandakan sebagai f-1. Fungsi songsang ialah suatu fungsi yag memetakan y kembali kepada x.


1. Fungsi ialah sejenis hubungan khas yang mana setiap objek dalam domain mempunyai hanya satu imej dalam kodomain.


Hubungan satu dengan satu Hubungan satu dengan satu
ialah fungsi ialah fungsi
2. Fungsi nilai mutlak ditakrifkan oleh
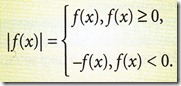

Graf fungsi nilai mutlak
3. Jika f ialah suatu fungsi yang memetakan set A kepada set B dan g ialah suatu fungsi yang memetakan set B kepada set C, maka gf ialah fungsi gubahan f diikuti dengan g yang memetakan set A terus kepada set C.

4. Jika

Bab 2 : Persamaan Kuadratik
1. Bentuk am persamaan kuadratik ialah
 yang mana:
yang mana:
1. Bentuk am persamaan kuadratik ialah
a, b dan c = pemalar
a ≠ 0
x = pembolehubah
2. Suatu persamaan kuadratik ax2 + bx + c = 0 dapat diselesaikan dengan
menggunakan kaedah:
3. Persamaan kuadratik dapat dituliskan sebagai

4. Bagi persamaan kuadratik ax2 + bx + c = 0,

5. Syarat untuk jenis punca persamaan kuadratik ialah
6.

3. Persamaan kuadratik dapat dituliskan sebagai
4. Bagi persamaan kuadratik ax2 + bx + c = 0,

5. Syarat untuk jenis punca persamaan kuadratik ialah

6.

Bab 3 : Fungsi Kuadratik

2. Nilai maksimum atau minimum bagi suatu fungsi kuadratik f(x) = ax2 + bx + c dapat dicari dengan menggunakan kaedah penyempurnaan kuasa dua, iaitu dengan mengungkapkan ax2 + bx + c dalam bentuk a(x + p)2 + q.
3. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai minimum. Nilai minimum itu ialah q dan ini berlaku apabila x = –p.

4. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai maksimum. Nilai maksimum itu ialah q dan ini berlaku apabila x = –p.

5. Bagi fungsi kuadratik f(x) = ax2 + bx + c = a(x + p)2 + q, persamaan paksi simetri ialah
6. Ketaksamaan kuadratik dapat diselesaikan dengan menggunakan kaedah lakaran graf seperti berikut.

2. Nilai maksimum atau minimum bagi suatu fungsi kuadratik f(x) = ax2 + bx + c dapat dicari dengan menggunakan kaedah penyempurnaan kuasa dua, iaitu dengan mengungkapkan ax2 + bx + c dalam bentuk a(x + p)2 + q.
3. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai minimum. Nilai minimum itu ialah q dan ini berlaku apabila x = –p.

4. Apabila a > 0, fungsi a(x + p)2 + q mempunyai nilai maksimum. Nilai maksimum itu ialah q dan ini berlaku apabila x = –p.

5. Bagi fungsi kuadratik f(x) = ax2 + bx + c = a(x + p)2 + q, persamaan paksi simetri ialah
6. Ketaksamaan kuadratik dapat diselesaikan dengan menggunakan kaedah lakaran graf seperti berikut.

Bab 5 : Indeks dan Logaritma
1. Hukum-hukum indeks ialah:
2. Indeks pecahan : 3. Indeks negatif :


4. Jika ax = y dengan keadaan a > 0, a ≠ 1, maka x ialah logaritma bagi y kepada asas a, iaitu
5. 6.

7. Hukum-hukum logaritma ialah

8.

9. Logaritma sesuatu nombor pada suatu asas tertentu boleh ditukarkan kepada asas yang lain dengan menggunakan rumus-rumus

10. Persamaan indeks
Jika an = bn, dengan keadaan a > 0, b > 0 atau a < 0, b < 0, maka
11. Persamaan logaritma
Jika maka x = y.
maka x = y.
1. Hukum-hukum indeks ialah:

2. Indeks pecahan : 3. Indeks negatif :
4. Jika ax = y dengan keadaan a > 0, a ≠ 1, maka x ialah logaritma bagi y kepada asas a, iaitu
5. 6.
7. Hukum-hukum logaritma ialah

8.
9. Logaritma sesuatu nombor pada suatu asas tertentu boleh ditukarkan kepada asas yang lain dengan menggunakan rumus-rumus

10. Persamaan indeks
Jika an = bn, dengan keadaan a > 0, b > 0 atau a < 0, b < 0, maka
11. Persamaan logaritma
Jika
Bab 6 : Geometri Koordinat
1. Jarak = 2. Titik tengah =

3. Koordinat titik yang membahagi secara dalam tembereng garis dengan nisbah m : n ialah
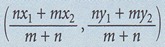
4. Luas segitiga =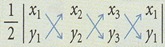
5. Luas sisiempat =
6. Kecerunan = @
@
7. Persamaan garis lurus ialah

9. Terdapat 3 jenis syarat yang menentukan persamaan lokus satu titik bergerak P(x,y):
(a) Jaraknya dari satu titik tetap, Q(x1, y1) ialah satu pemalar (k).
(b) Jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) adalah sama.
(c) Nisbah jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) ialah m : n.
1. Jarak = 2. Titik tengah =
3. Koordinat titik yang membahagi secara dalam tembereng garis dengan nisbah m : n ialah
4. Luas segitiga =
5. Luas sisiempat =
6. Kecerunan =
7. Persamaan garis lurus ialah
- jika kecerunan, m dan satu titik, (x1, y1) diberi,
- jika dua titik, (x1, y1) dan (x2, y2) diberi,
- jika pintasan-x, a dan pintasan-y, b diberi,

9. Terdapat 3 jenis syarat yang menentukan persamaan lokus satu titik bergerak P(x,y):
(a) Jaraknya dari satu titik tetap, Q(x1, y1) ialah satu pemalar (k).

(b) Jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) adalah sama.

(c) Nisbah jaraknya dari dua titik tetap, Q(x1, y1) dan R(x2, y2) ialah m : n.

Bab 7 : Statistik
1.

2. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka
3. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka
4. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka
5. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka
6. Apabila dua set data, X dan Y digabungkan, maka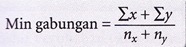

1.


2. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka

3. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka

4. Jika setiap cerapan dalam set data ditambah atau ditolak dengan satu nilai pemalar k, maka

5. Jika setiap cerapan dalam set data didarab dengan satu pemalar k, maka

6. Apabila dua set data, X dan Y digabungkan, maka

Bab 8 : Sukatan Membulat
1. Rumus penukaran darjah kepada radian ialah
2. Rumus penukaran radian kepada darjah ialah
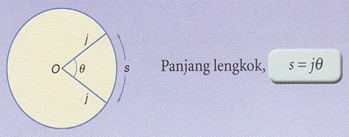
3.
4.
5.
1. Rumus penukaran darjah kepada radian ialah

2. Rumus penukaran radian kepada darjah ialah

3.

4.

5.

Bab 9 : Pembezaan
1. Terbitan pertama bagi suatu fungsi y terhadap x ialah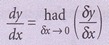
2, Jika y = uv, maka
3. Jika![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgRcATpFtSPlVoVkHjTLiH2o-TSw25VkP_XtYlCi8bJuZKfw0znaTPKVVPG3niGIiDLufTHm2PfZFwWUaT0QjHeOtPnvOBQkQOo9rwcdyUFBiL-qPmcgKjgPFmrNMnwe4dKf8unAieqixSA/?imgmax=800) , maka
, maka
4. Jika y = k[f(x)]n, maka
5. Jika y = f(u) dan u = g(x), maka

6. Persamaan tangen pada titik (x1, y1) ialah

7. Persamaan normal pada titik (x1, y1) ialah

8. Pada titik pusingan,
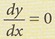
9. Pada titik maksimum, 10. Pada titik minimum,


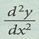
 adalah negatif. adalah positif.
adalah negatif. adalah positif.
11. Masalah Maksimum dan Minimum
12. Kadar Perubahan yang Terhubung
13. Perubahan Kecil
14. Penghampiran
1. Terbitan pertama bagi suatu fungsi y terhadap x ialah
2, Jika y = uv, maka

3. Jika

4. Jika y = k[f(x)]n, maka

5. Jika y = f(u) dan u = g(x), maka

6. Persamaan tangen pada titik (x1, y1) ialah
7. Persamaan normal pada titik (x1, y1) ialah
yang mana
8. Pada titik pusingan,
9. Pada titik maksimum, 10. Pada titik minimum,
dan tanda dan tanda
11. Masalah Maksimum dan Minimum

12. Kadar Perubahan yang Terhubung

13. Perubahan Kecil

14. Penghampiran

Bab 10 : Penyelesaian Segitiga
1.
Petua sinus diberi oleh
atau

2. Petua Sinus melibatkan Kes Berambiguiti

3. Petua Kosinus diberi oleh

4. Luas segitiga ABC

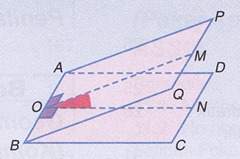
5. Geometri Tiga Matra
(a)

(b)

1.

Petua sinus diberi oleh
atau
2. Petua Sinus melibatkan Kes Berambiguiti

3. Petua Kosinus diberi oleh

4. Luas segitiga ABC

5. Geometri Tiga Matra
(a)

(b)




mntk izin print nota ni utk dijadikan rujukan ..
ReplyDelete